Latest ●  Object Manipulation ●  Sensor Coverage ●  Multi-Robot Motion Planning ●  Target Assignment ●  Informative Path Planning ●  Situational Awareness ●  Distributed Consensus

Optimal Multi-Sensor Coverage

Optimal Guarding of 3D Embedded Surfaces

We carry out a structural and algorithmic study of a mobile sensor coverage optimization problem targeting 2D surfaces embedded in a 3D workspace. The investigated settings model multiple important applications including camera network deployment for surveillance, geological monitoring/survey of 3D terrains, and UVC-based surface disinfection for the prevention of the spread of disease agents (e.g., SARS-CoV2). Under a unified general “sensor coverage” problem, three concrete formulations are examined, focusing on optimizing visibility, single-best coverage quality, and cumulative quality, respectively. After demonstrating the computational intractability of all these formulations, we describe approximation schemes and mathematical programming models for near-optimally solving them. The effectiveness of our methods is thoroughly evaluated under realistic and practical scenarios.

video ●  code ●  paper

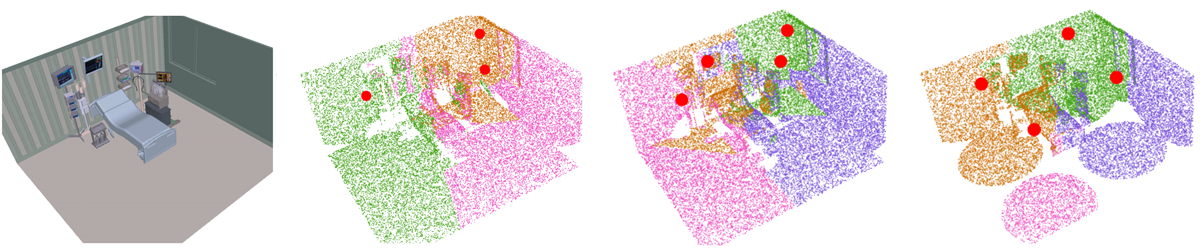
Sensor Placement for Globally Optimal Coverage of 3D-Embedded Surfaces. S. W. Feng, 
K. Gao, J. Gong, and J. Yu. 2021 IEEE International Conference on Robotics and 
Automation (ICRA 2021).

---

Optimal Region Guarding

We investigate the problem of using mobile robots equipped with 2D range sensors to optimally guard perimeters or regions. Given a bounded set in $\mathbb R^2$ to be guarded, and $k$ mobile sensors where the $i$-th sensor can cover a circular region with a variable radius $r_i$, we seek the optimal strategy to deploy the $k$ sensors to fully cover the set such that max $r_i$ is minimized. On the side of computational complexity, we show that computing a $1.152$-optimal solution for guarding a perimeter or a region is NP-hard even when the set is a simple polygon or the boundary of a simple polygon, i.e., the problem is hard to approximate. The hardness result on perimeter guarding holds when each sensor may guard at most two disjoint perimeter segments. On the side of computational methods, for the guarding perimeters, we develop a fully polynomial time approximation scheme (FPTAS) for the special setting where each sensor may only guard a single continuous perimeter segment, suggesting that the aforementioned hard-toapproximate result on the two-disjoint-segment sensing model is tight. For the general problem, we first describe a polynomialtime $(2 + \varepsilon)$-approximation algorithm as an upper bound, applicable to both perimeter guarding and region guarding. This is followed by a high-performance integer linear programming (ILP) based method that computes near-optimal solutions. Thorough computational benchmarks as well as evaluation on potential application scenarios demonstrate the effectiveness of these algorithmic solutions.

video ●  paper

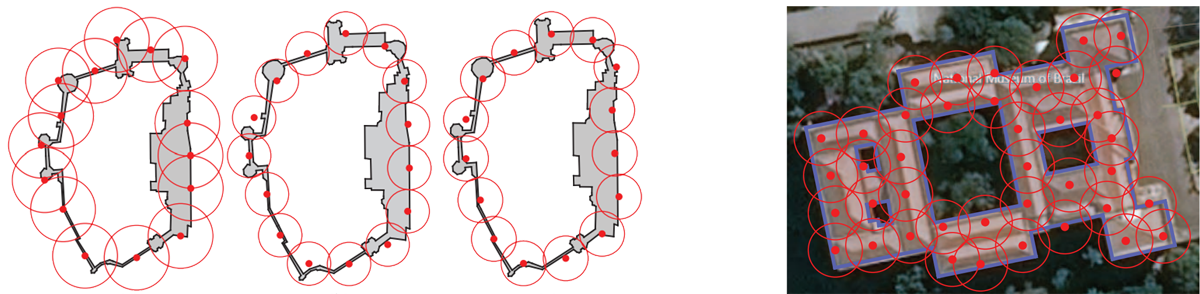
Optimally Guarding Perimeters and Regions with Mobile Range Sensors. 
S. W. Feng and J. Yu. 2020 Robotics: Science and Systems (RSS 2020).

---

Optimal Perimeter Guarding

We investigate the problem of optimally assigning a large number of robots (or other types of autonomous agents) to guard the perimeters of closed 2D regions, where the perimeter of each region to be guarded may contain multiple disjoint polygonal chains. Each robot is responsible for guarding a subset of a perimeter and any point on a perimeter must be guarded by some robot. In allocating the robots, the main objective is to minimize the maximum 1D distance to be covered by any robot along the boundary of the regions. For this optimization problem which we call optimal perimeter guarding (OPG), thorough structural analysis is performed, which is then exploited to develop fast exact algorithms that run in guaranteed low polynomial time. In addition to formal analysis and proofs, experimental evaluations and simulations are performed that further validate the correctness and effectiveness of our algorithmic results.

video ●  paper

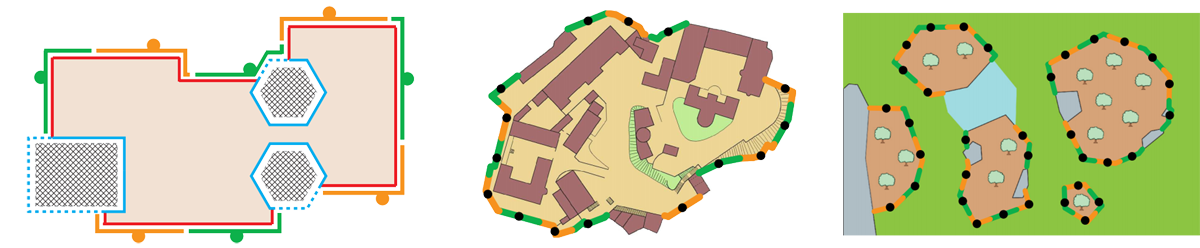
Efficient Algorithms for Optimal Perimeter Guarding. S. W. Feng, S. D. Han, 
K. Gao, and J. Yu. 2019 Robotics: Science and Systems (RSS 2019).

Heterogenerous sensors paper ● video

Optimal Perimeter Guarding with Heterogeneous Robot Teams: Complexity Analysis 
and Effective Algorithms. S. W. Feng and J. Yu. IEEE Robotics and Automation 
Letters, 5(2), page(s): 430-437, 2020.