Multi-Robot Motion Planning: Overview
Effectively coordinating the motion for a large number of robots or vehicles in crowded spaces is an important problem with applications to warehouse automation, traffic routing, among others. Adapting a graph-theoretical approach, one can show that feasibility tests can be completed in linear time and computing complete feasible solutions can be done in cubic time. The analysis boils down to the study of the structure of the permutation groups
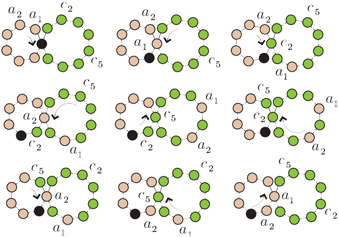 induced by synchronous robot motions. For example, the figure to the right illustrates how the locations of two robots ($c_2$ and $c_5$) may be exchanged on a cycle using a limited number of moves. For more details, see this paper.
induced by synchronous robot motions. For example, the figure to the right illustrates how the locations of two robots ($c_2$ and $c_5$) may be exchanged on a cycle using a limited number of moves. For more details, see this paper.
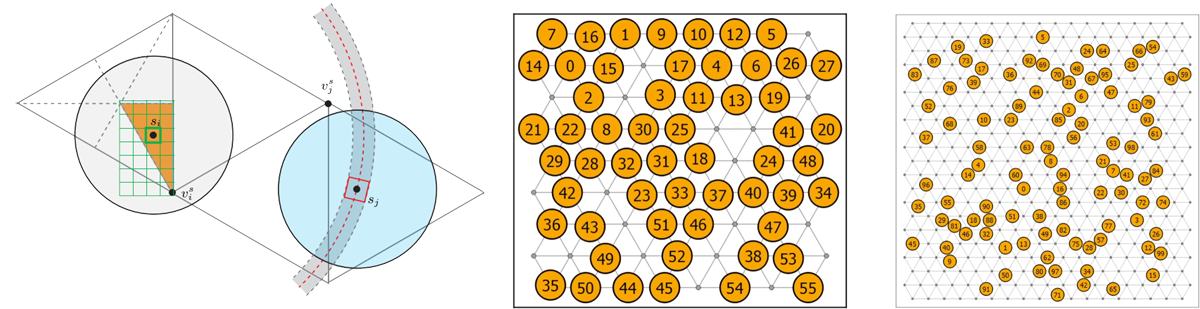
However, computing optimal or near-optimal solutions for such problems, in terms of minimizing task completion time or traveled distance, proves to be highly challenging as a computational problem. This is due to the curse of dimensionality: each robot introduces at least a few degrees of freedom. For $n$ robots, the search space is then $O(n)$ dimensional, which quickly becomes prohibitive to explore. Indeed, we could readily establish that common time- and distance-based objectives are NP-hard to optimize on general graphs, even planar ones. Different objectives generally cannot be optimized simultaneously.
On the other hand, because each robot mainly interacts with robots that are close by, decoupling of the search space is generally possible to some extent, unless the density of robots approaches the limit. Given the very high
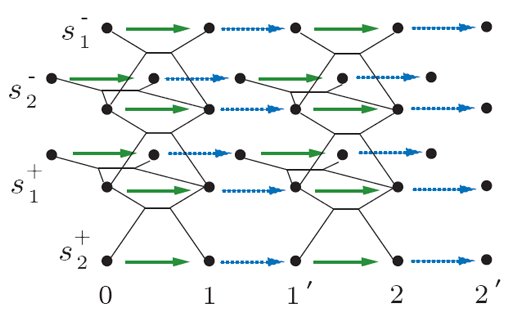 dimensional search space, we take the approach of early discretization and work with an extracted graph structure. By
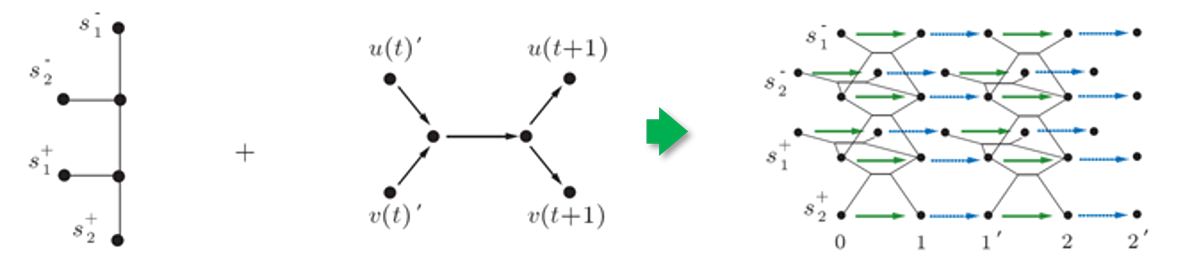
converting the problem into a multi-flow one
(see the figure to the left) and adapting a novel integer programming (ILP) based solution scheme, we are able to handle a broad spectrum of difficult problems, providing a leap in computational performance on multi-robot coordination problems. Using the graph-based method and an
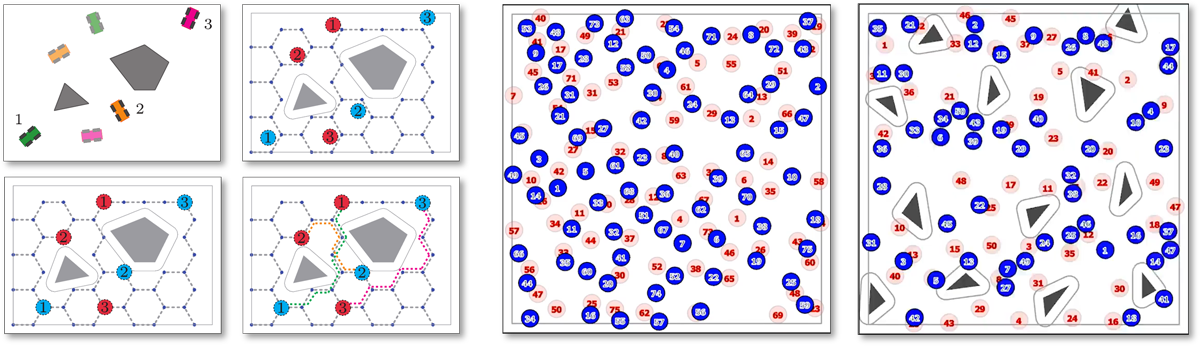
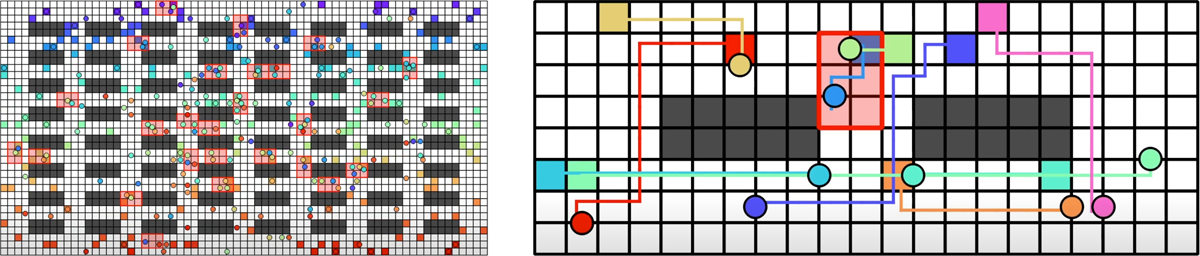
efficient discretization of continuous domains, we allow extremely dense setups with up to 30+% of free space occupied by
robots-our algorithms are capable of solving such instances within seconds for up to hundreds of robots while often ensuring 1.x-optimality (see the video). The source code of all current results can be found here.
dimensional search space, we take the approach of early discretization and work with an extracted graph structure. By
converting the problem into a multi-flow one
(see the figure to the left) and adapting a novel integer programming (ILP) based solution scheme, we are able to handle a broad spectrum of difficult problems, providing a leap in computational performance on multi-robot coordination problems. Using the graph-based method and an
efficient discretization of continuous domains, we allow extremely dense setups with up to 30+% of free space occupied by
robots-our algorithms are capable of solving such instances within seconds for up to hundreds of robots while often ensuring 1.x-optimality (see the video). The source code of all current results can be found here.
Topics
Computing Optimal Solutions
Solving Dense Continuous Problem with Provable Guarantees
Coordinating the Motion of Labeled Discs with Optimality Guarantees under Extreme
Density. R. Chinta, S. D. Han and J. Yu. Algorithmic Foundations of Robotics XIII,
Springer Proceedings in Advanced Robotics (SPAR), page(s): 817-834, 2020.
Toward Optimally Solving Continuous Problems
An Effective Algorithmic Framework for Near Optimal Multi-Robot Path Planning. J. Yu
and D. Rus. Bicchi A., Burgard W. (eds), Robotics Research, vol 1, pp 495-511, 2018.
Integer Programming Models and Heuristics
Optimal Multi-Robot Path Planning on Graphs: Complete Algorithms and Effective
Heuristics. J. Yu and S. M. LaValle. IEEE Transactions on Robotics, 32(5),
page(s): 1163 - 1177, 2016.
Multi-Robot Motion Planning on Graphs and Network Flow
<a id="links" href="/files/YuLav13STAR.pdf" target="_">paper</a>
Multi-agent Path Planning and Network Flow. J. Yu and S. M. LaValle. Algorithmic
Foundations of Robotics X, Springer Tracts in Advanced Robotics (STAR), Springer
Berlin/Heidelberg, vol 86, page(s): 157-173, 2013
Spatio-Temporal Splitting Heuristics for Speeding up MRMP Algorithms

Spatial and Temporal Splitting Heuristics for Multi-Robot Motion Planning. T. Guo,
S. D. Han, and J. Yu. 2021 IEEE International Conference on Robotics and Automation
(ICRA 2021).
Path Diversification and Database-Driven Conflict Resolution Heuristics
DDM: Fast Near-Optimal Multi-Robot Path Planning using Diversified-Path and
Optimal Sub-Problem Solution Database Heuristics. S. D. Han and J. Yu. IEEE
Robotics and Automation Letters 5, no. 2 (2020): 1350-1357.
Computational Complexity
NP-Hardness on Planar Graphs
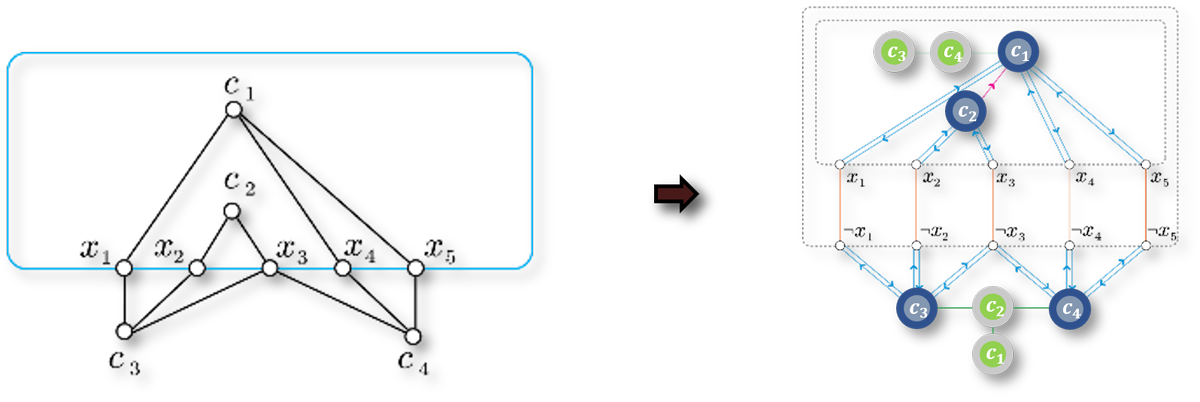
<a id="links" href="/files/Yu16RAL.pdf" target="_">paper</a>
Intractability of Optimal Multi-Robot Path Planning on Planar Graphs. J. Yu. IEEE
Robotics and Automation Letters, 1(1), page(s): 33-40, 2016.
NP-Hardness on General Graphs
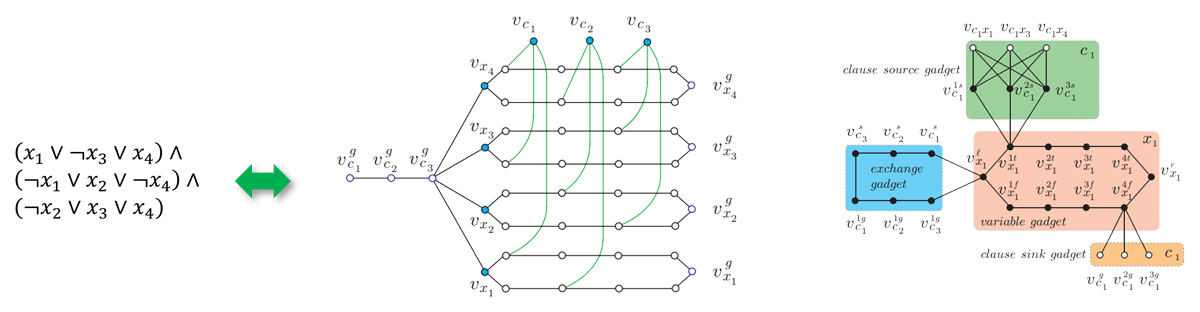
<a id="links" href="https://arxiv.org/pdf/1507.03289.pdf" target="_">paper</a>
Optimal Multi-Robot Path Planning on Graphs: Structure and Computational Complexity.
J. Yu and S. M. LaValle. arXiv, 2015.
Initial AAAI-13 conference paper
Structure and Intractability of Optimal Multi-robot Path Planning on Graphs. J. Yu
and S. M. LaValle. The Twenty-Seventh AAAI Conference on Artificial Intelligence, 2013.
Feasibility Issues
Feasbility via Group Theoretic Methods

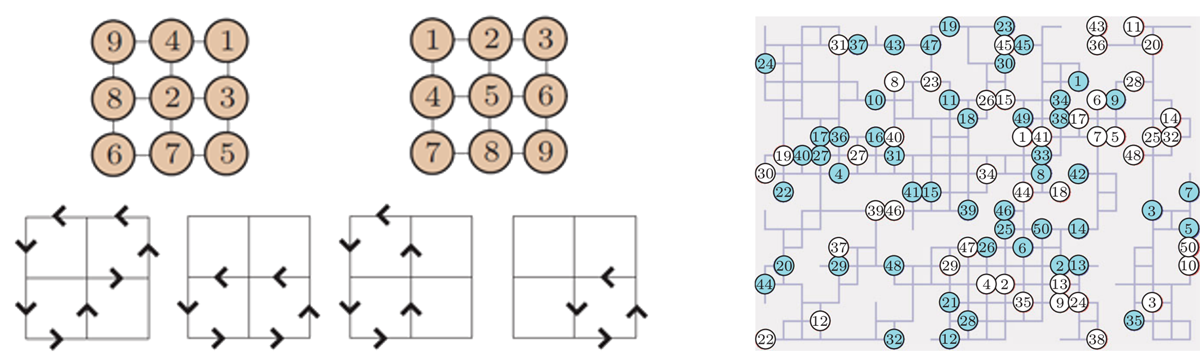
Let $G$ be a simple connected graph with $n$ vertices and let there be $p < n$ labeled pebbles. In a configuration, the pebbles occupy $p$ distinct vertices of $G$. From a configuration, a pebble may move to a nearby unoccupied vertex in one step. Now given two configurations $S$ and $D$, a natural question is whether $S$, $D$ are reachable from each other. Kornhauser, Miller, and Spirakis (FOCS 1984) showed that this problem can be decided in polynomial time but a solution may require $\Theta(n^3)$ moves. This suggests that no algorithm can solve all instances of the problem under cubic time. Therefore, deciding whether such a problem is feasible using less time helps avoiding unnecessary computations on infeasible instances. Auletta et al. (SWAT, 1996) worked on pebble motion on trees and provided a linear time algorithm for testing the feasibility of this problem. Observing that pebbles on a 2-edge-connected component are almost always equivalent, we reducethe pebble motion on graphs to the pebble motion on trees in linear time by contracting these components intoa single edge. We obtained this result independently of Goraly and Hassin, whose work imply a similar result.
Manuscript on arXiv:
A Linear Time Algorithm for the Feasibility of Pebble Motion on Graphs. J. Yu, 2013
Synchronous Pebble Motion on Graphs and Permutation Groups from Cyclic Rotations of Pebbles

|
Let $G$ be a simple connected graph with $n$ vertices and let there be $n$ labeled pebbles occupying these $n$ vertices. In each step, pebbles on disjoint cycles may rotate to occupy neighboring vertices (all pebbles on a cycle must rotate in the same direction). This allows the pebbles to be reconfigured. The reachable configurations form a group depending only on the graph $G$. We show that such a group has a diameter no more than $O(n^2)$. Using this intermediate result, we can also extend results on the pebble motion problem (which may have unoccupied vertices but does not allow rotations) to this synchronous pebble motion formulation. Synchronous pebble motion is a more natural model for multi-robot path planning on graphs since robots should be able to move synchronously without a swap space. Synchronous problem can be solved in polynomial time. In particular, similar to the pebble motion problem, feasibility test of this problem can be done in linear time. |
Pebble Motion on Graphs with Rotations: Efficient Feasibility Tests and Planning
Algorithms. J. Yu and Daniela Rus. Algorithmic Foundations of Robotics XI,
Springer Tracts in Advanced Robotics (STAR), vol 107, page(s): 729-746, 2015.