Optimal Target Assignement: Overview
A special but rather important case in multi-robot coordination is when all robots are interchangeable. For example, consider the case of dispatching servicing robots with the same functionality. It does not matter which robot
serves which request. In such cases, the coordination problem appear to become more difficult at a first glance because it is not immediately clear which robot should handle which task. As it turns out, the problem is in fact
simpler because the
existence of a natural ordering which induces a DAG structure in the planning domain. Starting with a graph-based problem, we
provide algorithmic solutions that, through separating goal assignment and path planning/coordination, solving the assignemnt and coordination problem with a total running time of
$O(n^2V)$, in which $n$ is the number of robots and $V$ is the number of vertices of the graph. We further show that distance optimal paths can also be scheduled with a completion (convergence) time of no more than $n + V - 1$, which
is a tight bound. The resulting algorithm is fast enough to plan distance  optimal paths for hundreds of robots in near real time, as we demonstrated
with a java applet application.
In a followup work, we show that after initial paths are planned, path execution can be achieved using only local, distance two communication between the robots. Recently, the graph-based
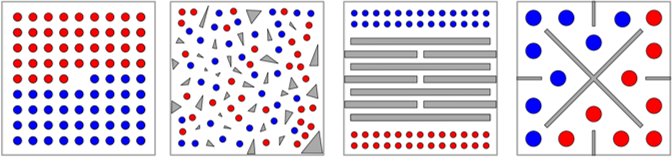
results are extended to continuous domain with similar optimality guarantees. A typical example here is illustrated in the figure to the right, in which many robots must move from the blue
locations to the red locations with optimality assurance. More recently, we have further extended the work to continuous domains under a stochastic setting,
establishing that locally optimal behavior can give rise to near-optimal global behavior.
optimal paths for hundreds of robots in near real time, as we demonstrated
with a java applet application.
In a followup work, we show that after initial paths are planned, path execution can be achieved using only local, distance two communication between the robots. Recently, the graph-based
results are extended to continuous domain with similar optimality guarantees. A typical example here is illustrated in the figure to the right, in which many robots must move from the blue
locations to the red locations with optimality assurance. More recently, we have further extended the work to continuous domains under a stochastic setting,
establishing that locally optimal behavior can give rise to near-optimal global behavior.
Topics
Distance Optimal Target Assignment in Robotic Networks
<a id="links" href="/files/YuChuVou15TAC.pdf" target="_">paper</a>
Target Assignment in Robotic Networks: Distance Optimality Guarantees and Hierarchical
Strategies. J. Yu, S.-J. Chung, and P. G. Voulgaris. IEEE Transactions on Automatic
Control, 60(2), page(s): 327-341, 2015.
Optimal Unlabled Multi-Robot Motion Planning in Continuous Domains
<a id="links" href="/files/SolYuZamHal15RSS.pdf" target="_">paper</a>
Motion Planning for Unlabeled Discs with Optimality Guarantees. K. Solovey, J. Yu, O.
Zamir, and D. Halperin. 2015 Robotics: Science and Systems (RSS 2015).
Optimal Unlabled Multi-Robot Motion Planning on Graphs

Distance Optimal Formation Control on Graphs with a Tight Convergence Time Guarantee.
J. Yu and S. M. LaValle. The 51st IEEE Conference on Decision and Control (CDC 2012).
Shortest Path Set Induced Vertex Ordering and its Application to Distributed Distance
Optimal Formation Planning and Control on Graphs. J. Yu and S. M. LaValle. 52nd IEEE
Conference on Decision and Control (CDC 2013).