Latest ●  Object Manipulation ●  Sensor Coverage ●  Multi-Robot Motion Planning ●  Target Assignment ●  Informative Path Planning ●  Situational Awareness ●  Distributed Consensus

Informative Path Planning: Overview

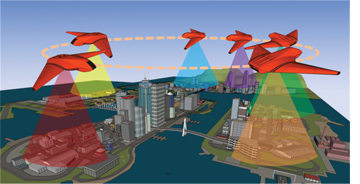As mobile robots get deployed to perform sensing tasks (e.g., surveillance, monitoring, scientific exploration), there are usually multiple objectives that must be properly balanced. The general goal is to plan paths and policies that best suit the goal of the mission. Often, it is not clear whether multiple goals can be simultaneously optimized. With the question in mind, we began examining a broad class of problems in which multiple Poisson processes are spatially distributed, mimicking temporally-driven random events to be observed. To observe these events, a mobile robot (observer) must travel to the event site. Because the events are transient (i.e., time sensitive), the longer the robot waits at a particular site, the more likely it will be able to observe the particular event. Therefore, to observe a balanced portfolio of events, the robots must weigh between frequently traveling between different sites and staying at each site longer for making more observations. As it turns out, under proper (and mild) conditions, as established in this paper, there exists a globally optimal policy for scheduling the trip of the robot to (i) maximize the number of events observed and (ii) minimize the delay between consecutive observations of events occurring at the same site. Assuming a cyclic patrol policy is used, we provide a polynomial time approximation scheme (PTAS) that computes for any $\varepsilon > 0$ a $(1+\varepsilon)$-optimal solution for the more general, NP-hard problem. Beside this persistent monitoring problem, we have also studied several related problems including the Correlated Orienteering Problem and the Optimal Tourist Problem.

Topics

The Optimal Tourist Problem

The Optimal Tourist Problem (OTP), named in the same spirit as the Traveling Salesperson Problem (TSP), formulates the problem in which a mobile sensing robot is tasked to travel among and gather intelligence at a set of spatially distributed point-of-interests (POIs). The quality of the information collected at each POI is characterized by some sensory (reward) function of time. With limited fuel, the robot must balance between spending time traveling to more POIs and performing time-consuming sensing activities at the visited POIs to maximize the overall reward. In a dual formulation, the robot may be required to acquire a minimum mount of reward with the least amount of time. We propose an anytime planning algorithm for solving these two NP-hard problems to arbitrary precision for arbitrary reward functions. Our algorithm is effective on large instances with tens to hundreds of POIs, as demonstrated with an extensive set of computational experiments. Besides mobile sensor scheduling, the algorithm also applies to automation scenarios such as intelligent and optimal itinerary planning, as the name implies.

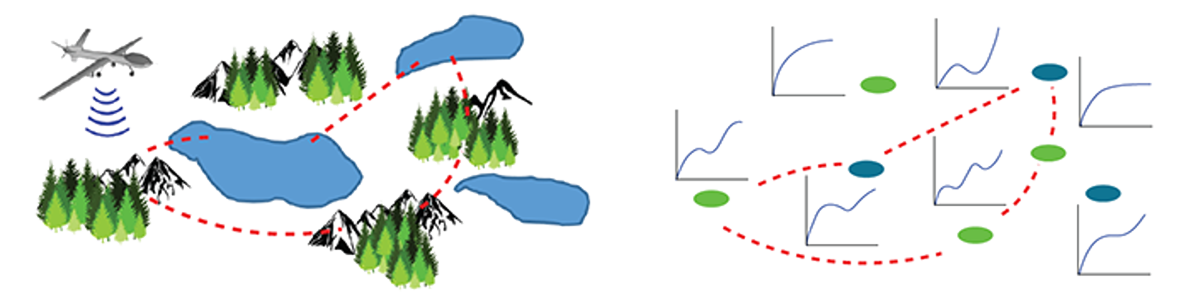
Note that OTP does not contain a stochastic element as the somewhat similar persistent monitoring formulation (stated below). It turns out that the non-stochastic nature actually makes OTP actually much harder.

 <a id="links" href="/files/YuAslKarRus15IROS.pdf" target="_">paper</a> 

Anytime Planning of Optimal Schedules for a Mobile Sensing Robot. J. Yu, 
J. Aslam, S. Karaman, and D. Rus. 2015 IEEE/RSJ International Conference 
on Intelligent Robots and Systems (IROS 2015).

---

The Correlated Orienteering Problem

We propose the correlated orienteering problem (COP) as a novel nonlinear extension to the classic orienteering problem (OP). With the introduction of COP, it becomes possible to model the planning of informative tours for the persistent monitoring of a spatiotemporal field with time-invariant spatial correlations using autonomous mobile robots, in which the robots are range- or time-constrained. Our focus in this paper is QCOP, a quadratic COP instantiation that looks at correlations between neighboring nodes in a node network. The main feature of QCOP is a quadratic utility function capturing the said spatial correlation. We solve QCOP using mixed integer quadratic programming, with the resulting anytime algorithm capable of planning multiple disjoint tours that maximize the quadratic utility. In particular, our algorithm can quickly plan a near-optimal tour over a network with up to 150 nodes. Beside performing extensive simulation studies to verify the algorithm’s correctness and characterize its performance, we also successfully applied QCOP to two realistic persistent monitoring tasks: 1) estimation over a synthetic spatiotemporal field and 2) estimating the temperature distribution in the state of Massachusetts in the United States.

code ●  paper

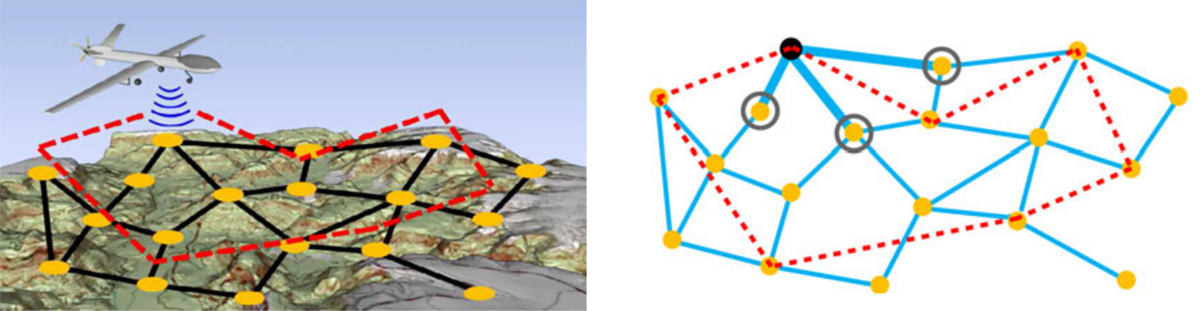
Correlated Orienteering Problem and its Application to Persistent Monitoring 
Tasks. J. Yu, M. Schwager, and D. Rus. IEEE Transactions on Robotics, 32(5), 
page(s): 1106 - 1118, 2016.

---

Persistent Monitoring of Stochastic Events

We introduce a new mobile sensor scheduling problem involving a robot tasked to monitor several events occurring at spatially distributed locations. Of particular interest is the monitoring of transient events of stochastic nature, with applications ranging from natural phenomena (e.g., monitoring abnormal seismic activity around a volcano using a ground robot) to urban activities (e.g., monitoring early formations of traffic congestion using an aerial robot). Here, these stochastic arrival processes are modeled as an independent Poisson processes with various inter-arrival rates.

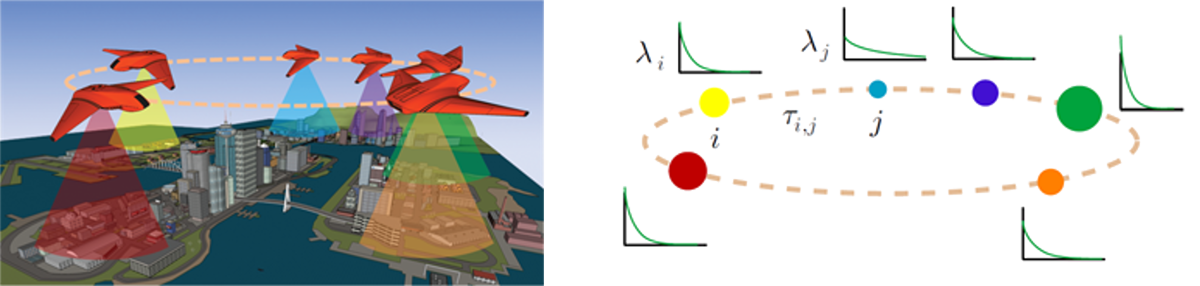
In monitoring such events, the robot seeks to: (i) maximize the number of events observed and (ii) minimize the delay between consecutive observations of events occurring at the same location. We are interested in finding a cyclic patrolling route that that optimizes these objectives in a balanced manner. To tackle the problem, first, assuming the cyclic ordering of stations is known, we prove the existence and uniqueness of the optimal solution, and show that the solution has desirable convergence rate and robustness. Our constructive proof also yields an efficient algorithm for computing the unique optimal solution with linear time complexity. The analysis remains valid when the cyclic order is unknown. We then provide a polynomial-time approximation scheme that computes for any $\varepsilon > 0$ a $(1+\varepsilon)$-optimal solution for the more general, NP-hard problem in which the order of the stations is unknown.

 <a id="links" href="/files/YuKarRus15TOR.pdf" target="_">paper</a> 

Persistent Monitoring of Events with Stochastic Arrivals at Multiple Stations. 
J. Yu, S. Karaman, and D. Rus. IEEE Transactions on Robotics, 31(3), page(s): 
521-535, 2015.