Latest ●  Object Manipulation ●  Sensor Coverage ●  Multi-Robot Motion Planning ●  Target Assignment ●  Informative Path Planning ●  Situational Awareness ●  Distributed Consensus

Selected Recent Research

This page was last updated in 2021; we are falling behind in keeping it updated as we are making rapid progress in a few areas. Please check our publications page for recent research.

Running Buffer Minimization

For tabletop rearrangement problems with overhand grasps, storage space outside the tabletop workspace, or buffers, can temporarily hold objects which greatly facilitates the resolution of a given rearrangement task. This brings forth the natural question of how many running buffers are required so that certain classes of tabletop rearrangement problems are feasible. We examine the problem for both the labeled and the unlabeledsettings. We observe that finding the minimum number of running buffers (MRB) can be carried out on a dependency graph abstracted from a problem instance, and show that computing MRB on dependency graphs is NP-hard. The number of required running buffers may grow unbounded as the number of objects to be rearranged increases even for uniform cylinders. On the algorithmic side, we develop highly effective algorithms for finding MRB for both labeled and unlabeled tabletop rearrangement problems, scalable to over a hundred objects under very high object density. Employing these algorithms, empirical evaluations show that random labeled and unlabeled instances, which more closely mimics real-world setups, have much smaller MRBs.

read more ●  video ●  code ●  paper

On Minimizing the Number of Running Buffers for Tabletop Rearrangement. K. Gao,
S. W. Feng, and J Yu. 2021 Robotics: Science and Systems (RSS 2021).

---

Rearrangement on Lattices

We propose and study a class of rearrangement problems under a novel pick-n-swap prehensile manipulation model, in which a robotic manipulator, capable of carrying an item and making item swaps, is tasked to sort items stored in lattices of variable dimensions in a time-optimal manner. We systematically analyze the intrinsic optimality structure, which is fairly rich and intriguing, under different levels of item distinguishability (fully labeled, where each item has a unique label, or partially labeled, where multiple items may be of the same type) and different lattice dimensions. Focusing on the most practical setting of one and two dimensions, we develop low polynomial time cycle-following based algorithms that optimally perform rearrangements on 1D lattices under both fully- and partially-labeled settings. On the other hand, we show that rearrangement on 2D and higher dimensional lattices becomes computationally intractable to optimally solve. Despite their NP-hardness, we prove that efficient cycle-following based algorithms remain asymptotically optimal for 2D fully- and partially-labeled settings, in expectation, using the interesting fact that random permutations induce only a small number of cycles. We further improve these algorithms to provide 1.x-optimality when the number of items is small. Simulation studies corroborate the effectiveness of our algorithms.

read more ●  video ●  poster ●  code ●  paper

Rearrangement on Lattices with Pick-n-Swaps: Optimality Structures and Efficient 
Algorithms. J. Yu. 2021 Robotics: Science and Systems (RSS 2021). 

---

Deep Interaction Prediction

We propose a Deep Interaction Prediction Network (DIPN) for learning to predict complex interactions that ensue as a robot end-effector pushes multiple objects, whose physical properties, including size, shape, mass, and friction coefficients may be unknown a priori. DIPN “imagines” the effect of a push action and generates an accurate synthetic image of the predicted outcome. DIPN is shown to be sample efficient when trained in simulation or with a real robotic system. The high accuracy of DIPN allows direct integration with a grasp network, yielding a robotic manipulation system capable of executing challenging clutter removal tasks while being trained in a fully self-supervised manner. The overall network demonstrates intelligent behavior in selecting proper actions between push and grasp for completing clutter removal tasks and significantly outperforms the previous state-of-the-art. Remarkably, DIPN achieves even better performance on the real robotic hardware system than in simulation.

read more ●  video ●  code ●  paper

DIPN: Deep Interaction Prediction Network with Application to Clutter Removal. 
B. Huang, S. D. Han, A. Boularias, and J. Yu. 2021 IEEE International Conference 
on Robotics and Automation (ICRA 2021).

---

Globally Optimal Coverage of 3D-Embedded Surfaces

We carry out a structural and algorithmic study of a mobile sensor coverage optimization problem targeting 2D surfaces embedded in a 3D workspace. The investigated settings model multiple important applications including camera network deployment for surveillance, geological monitoring/survey of 3D terrains, and UVC-based surface disinfection for the prevention of the spread of disease agents (e.g., SARS-CoV2). Under a unified general “sensor coverage” problem, three concrete formulations are examined, focusing on optimizing visibility, single-best coverage quality, and cumulative quality, respectively. After demonstrating the computational intractability of all these formulations, we describe approximation schemes and mathematical programming models for near-optimally solving them. The effectiveness of our methods is thoroughly evaluated under realistic and practical scenarios.

video ●  code ●  paper

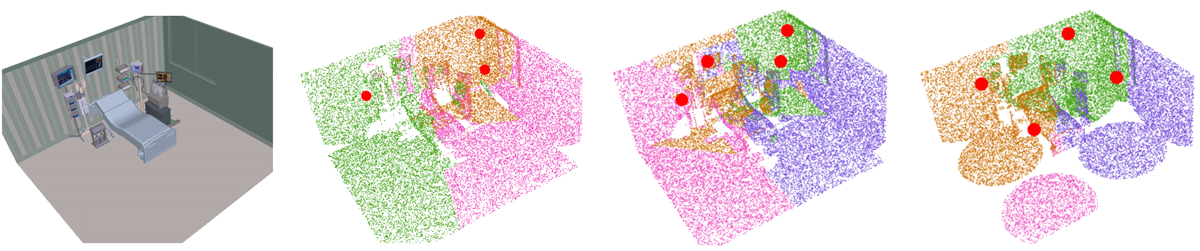
Sensor Placement for Globally Optimal Coverage of 3D-Embedded Surfaces. S. W. Feng, 
K. Gao, J. Gong, and J. Yu. 2021 IEEE International Conference on Robotics and 
Automation (ICRA 2021).

---

Spatio-Temporal Splitting Heuristics for MRMP

We examine the application of spatio-temporal splitting heuristics to the multi-robot motion planning (MRMP) problem in a graph-theoretic setting. Following the divide-and-conquer principle, we design multiple spatial and temporal splitting schemes that can be applied to any existing MRMP algorithm, in an orthogonal manner. The combination of a good baseline MRMP algorithm with a proper splitting heuristic proves highly effective, allowing the resolution of problems 10+ times than what is possible previously, as corroborated by extensive numerical evaluations. 5-15 times speedups are usually observed with little degradation to solution optimality.

video ●  paper

Spatial and Temporal Splitting Heuristics for Multi-Robot Motion Planning. T. Guo, 
S. D. Han, and J. Yu. 2021 IEEE International Conference on Robotics and Automation 
(ICRA 2021).

---

Rubik Table and Stack Rearrangement

There are $n \ge 2$ stacks, each filled with $d$ items, and one empty stack. Every stack has capacity $d > 0$. A robot arm, in one stack operation (step), may pop one item from the top of a non-empty stack and subsequently push it onto a stack not at capacity. In a labeled problem, all $nd$ items are distinguishable and are initially randomly scattered in the $n$ stacks. The items must be rearranged using pop-and-pushs so that in the end, the $k^{\rm th}$ stack holds items $(k-1)d +1, \ldots, kd$, in that order, from the top to the bottom for all $1 \le k \le n$. In an unlabeled problem, the $nd$ items are of $n$ types of $d$ each. The goal is to rearrange items so that items of type $k$ are located in the $k^{\rm th}$ stack for all $1 \le k \le n$. In carrying out the rearrangement, a natural question is to find the least number of required pop-and-pushes.

Our main contributions are: (1) an algorithm for restoring the order of $n^2$ items stored in an $n \times n$ table using only $2n$ column and row permutations, and its generalization, and (2) an algorithm with a guaranteed upper bound of $O(nd)$ steps for solving both versions of the stack rearrangement problem when $d \le \lceil cn \rceil$ for arbitrary fixed positive number $c$. In terms of the required number of steps, the labeled and unlabeled version have lower bounds $\Omega(nd + nd{\frac{\log d}{\log n}})$ and $\Omega(nd)$, respectively.

video ●  paper

On Rearrangement of Items Stored in Stacks. M. Szegedy and J. Yu. Algorithmic 
Foundations of Robotics XIV, Springer Proceedings in Advanced Robotics (SPAR), 
page(s): 518-833, 2021. Presented at WAFR 2020.